COLEGIO DE  BACHILLERATO

 “PONCE ENRÍQUEZ”

Nombre:                   

          

 Daniela Ocampo

Profesor:

                              

                        Eduardo Santin

Curso:

                               

                        1 ero ciencias

Materia:

                          

                          Desarrollo del pensamiento filosófico

Año lectivo: 

   2016-2017

SOBRE EL CAOS Y EL ORDEN DEL UNIVERSO

Es opinión común considerar el Caos como sinónimo de desorden y falta de acción.. Asociamos la falta de razón, la irracionalidad, con el Caos, e inmediatamente sentimos desagrado, como si todo lo que no fuese racional resultase negativo, caótico. Es una de las capacidades del hombre moderno, hijo del mundo científico que surge del Renacimiento, que es dueño de ordenar el mundo a gran escala. De ahí que todo lo que asociamos con desorden y falta de utilidad lo llamamos caótico, y lo clasificamos como negativo. No era esta la visión de los pueblos antiguos; a través de sus mitos y sus poemas nos han dejado una visión del mundo repleta de dioses y de fuerzas creadoras, que si bien no parece demasiado racional sí despiertan dentro nuestro a través de la poesía y de la intuición un mundo que nos resulta muy familiar. En esos mitos el Caos siempre aparece como la gran causa creadora, una especie de sustrato básico del cual surge el Orden, desde los dioses primordiales hasta la propia humanidad. Todo ellos está presente en el Caos, como de alguna forma misteriosa para nosotros el árbol está presente en la semilla.

Durante el siglo XX se ha producido toda una serie de revoluciones científicas que han dado nuevo interés a la visión tradicional y mítica del mundo. La paradoja del observador en la mecánica cuántica, el continuum del espacio-tiempo en la teoría de la Relatividad, eran semillas de un nuevo orden, menos rígido y determinista que el anterior, más irracional, más caótico.  Bajo esa nueva óptica los científicos han vuelto su mirada a los viejos mitos, observando que bajo las viejas historias había oculto un legado profundísimo de enseñanzas. A través de las siguientes líneas realizaremos un viaje a través de la ciencia y de la mitología, y rescataremos al Caos como gran potencialidad oculta de todas las cosas.

LA TEORÍA DE LA INCERTIDUMBRE DE HEISENBERG

Es natural pensar que si una partícula está localizada, debemos poder asociar con ésta un paquete de ondas más o menos bien localizado. Un paquete de ondas se construye mediante la superposición de un número infinito de ondas armónicas de diferentes frecuencias. En un instante de tiempo dado, la función de onda asociada con un paquete de ondas está dada por. 

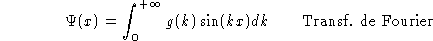
Donde k representa el número de onda

Donde que  representa el número de onda y donde la integral representa la suma de ondas con frecuencias (o número de ondas) que varían desde cero a más infinito ponderadas mediante el factor

El momento de la partícula y el número de ondas están relacionados ya que de lo cual se deduce que Queda claro que para localizar una partícula es necesario sumar todas las contribuciones de las ondas cuyo número de onda varía entre cero e infinito. Es decir que está completamente indeterminado. Para ilustrar lo anterior hemos indicado en la siguiente figura diferente

Tipos de paquetes de onda y su transformada de Fourier que nos dice como están distribuidas las contribuciones de las ondas con número de ondas Que k dentro del paquete. En el primer caso vemos que un paquete de ondas bien localizado en el

Espacio por, tiene contribuciones prácticamente iguales de todas las ondas con número de ondas que.

el número de ondas (o el momento) de la partícula.

El principio de incertidumbre nos dice que hay un límite en la precisión con el cual podemos determinar al mismo tiempo la posición y el momento de una partícula. La expresión matemática que describe el principio de incertidumbre de Heisenberg

En el segundo caso vemos que si relajamos un poco la posición del paquete de ondas, también es posible defin.

Benoit Mandelbrot

Benoit Mandelbrot, matemático polaco, falleció, como comentábamos el otro día, el pasado 14 de octubre, aunque hasta el día 16 no nos enteramos de esta triste noticia. Mandelbrot es, como a mí me gusta decir, el último grande, una de las pocas personas que ha sido capaces de crear una nueva rama de las matemáticas, la geometría fractal, con gran interés tanto por la teoría como por las aplicaciones de los resultados obtenidos.

Notas biográficas

Benoit Mandelbrot nació en Varsovia el 20 de noviembre de 1924 dentro de una familia con cierta tradición académica (aunque su padre se ganaba la vida con la compra-venta de ropa). Fueron dos tíos suyos quienes se encargaron de introducir a Mandelbrot en el mundo de las matemáticas. Uno de ellos, Solen Mandelbrojt, se encargó de su educación cuando la familia Mandelbrot emigró a Francia en 1936. El hecho de que Mandelbrot estudiara en la época de la Primera Guerra Mundial, entre otras cosas, provocó que su educación no fuera convencional. El propio Mandelbrot atribuye gran parte de su éxito matemático a esta educación poco convencional, ya que ello le permitió pensar de forma distinta a la que se le suele inculcar a quien sigue la educación habitual. Su gran visión e intuición geométrica también contribuyeron a ello.

Después de estudiar en Lyon y permanecer un día en la École Normale de París, Mandelbrot comenzó sus estudios en la École Polytechnique en 1944 bajo la dirección de Paul Lévy, quien también ejerció gran influencia en él. Más adelante se doctoró en la Universidad de París y viajó a Estados Unidos, donde, entre otras cosas, fue el último estudiante de postdoctorado de John Von Neumann. Echando un ojo a los mentores de Mandelbrot podemos ver que la lista no tiene desperdicio, si uno era bueno el siguiente era mejor. A lo largo de su vida fue profesor en la Universidad de Harvard y en la Universidad de Yale (donde terminó su carrera), entre otras instituciones. Pero posiblemente fue su trabajo en IBM en el Centro de Investigaciones Thomas B. Watson de Nueva York lo que más le ayudó en sus estudios, ya que allí le brindaron libertad total en sus investigaciones.

¿Cuánto mide la costa de Gran Bretaña?

Benoit Mandelbrot es el padre de la denominada Geometría Fractal, una nueva rama de la geometría que podemos decir que estudia los objetos tal como son. Mandelbrot pensó que las cosas en la realidad no son tan perfectas como las muestra la geometría elucídela: las esferas no son realmente esferas, las líneas no son perfectamente rectas, las superficies no son uniformes… Ello le llevó a estudiar estas imperfecciones, derivando estos estudios en la creación de esta nueva rama de la geometría. Las primeras ideas sobre fractales de Mandelbrot fueron publicadas en la revista Sáciense en 1967 a través de su artículo ¿Cuánto mide la costa de Gran Bretaña? En él da ciertas evidencias empíricas de que la longitud de una línea geográfica (como por ejemplo, la costa de Gran Bretaña) depende de la regla con la que la midamos.  

z₁ = (z₀)² + z₀
 z₂ = (z₁)² + z₀

 z₃ = (z₂)² + z₀                                                                                                                                                                                                       

Los honores

Mandelbrot recibió a lo largo de su vida innumerable honores y premios. Algunos de ellos son: la medalla Burnard en 1985 por sus servicios extraordinarios a la ciencia; la medalla Franklin en 1986; el premio Alexander von Humboldt en 1987; la medalla Steinmetz en 1988; la Legión de Honor en 1989; la medalla Nevada en 1991; el premio Wolf de Física en 1993; y el Premio Japón de Ciencia y Tecnología en 2003.

Conclusión

Heisenberg pasó a considerar un segundo problema: cómo describir la posición de la partícula. ¿Cuál es el procedimiento indicado para determinar dónde está una partícula? La respuesta obvia es ésta: observarla. Pues bien, imaginemos un microscopio que pueda hacer visible un electrón. Si lo queremos ver debemos proyectar una luz o alguna especie de radiación apropiada sobre él. Pero un electrón es tan pequeño, que bastaría un solo fotón de luz para hacerle cambiar de posición apenas lo tocara. Y en el preciso instante de medir su posición, alteraríamos ésta. Aquí nuestro artificio medidor es por lo menos tan grande como el objeto que medimos; y no existe ningún agente medidor más pequeño que el electrón. En consecuencia, nuestra medición debe surtir, sin duda, un efecto nada desdeñable, un efecto más bien decisivo en el objeto medido. Podríamos detener el electrón y determinar así su posición en un momento dado. Pero si lo hiciéramos, no sabríamos cuál es su movimiento ni su velocidad. Por otra parte, podríamos gobernar su velocidad, pero entonces no podríamos fijar su posición en un momento dado.

Heisenberg demostró que no nos será posible idear un método para localizar la posición de la partícula subatómica mientras no estemos dispuestos a aceptar la incertidumbre absoluta respecto a su posición exacta. Es un imposible calcular ambos datos con exactitud al mismo tiempo.